Probable Marks in board exam: 17
Above probable marks means : In board exam questions asked form this chapter are nearly for 17 marks out of 50 Marks.
Scope of the Syllabus
- Introduction to data structures.
- Data structure operations.
- Algorithmic notations.
- Control structures.
- Arrays-Representation in memory, Traversing, Deleting, Sorting, Binary search in an array, Pointer arrays, Records in memory using array.
- Linked list – Representation in memory
- Trees, Binary trees – Representing binary tree in memory.
Q. 8 Explain Repeat-While structure.
Ans : The repeat-while loop has the form :
Repeat While condition : [module] [End of loop]
Here, body of loop i.e. module is executed repeatedly, unit the condition is satisfied.
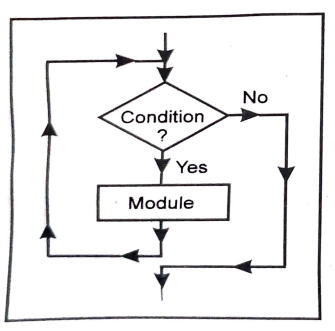
There must be a statement before the structure that initializes the condition controlling the loop and there must be a statement in the body of the loop that changes the condition.
For e.g. Find largest element in array.
Given a nonempty array DATA with N numerical values. This algorithm finds the location LOC and the value MAX of the largest element of DATA
1. Set K := 1, LOC := 1, MAX : = DATA[1] 2. Repeat step 3 and 4 while K <= N: 3. If MAX < DATA [K], then: set LOC := K and set MAX := DATA[K] [End of If structure] 4. Set K := K +1 [End of step 2 loop] 5. Write : LOC, MAX 6. Exit
Q.9 Explain with flowcharts the following control structures :
(i) Sequence logic, (ii) Selection logic, (iii)Iteration logic
Ans :
(i) Sequence logic :
In the sequence logic modules are executed sequentially, one after the another. The sequence may be present explicitly by means of numbered step or by the order in which modules are written.
(ii) Selection logic :
Selection logic uses number of conditions, which cause selection of one out of several alternative modules.
(a) Single alternative :
If condition is satisfied then module A, which consists of number of statements, is executed. Otherwise module A is skipped and next module is executed.

(b) Double alternative :
If the condition is satisfied, then module A will be executed otherwise module B will be executed.

(c) Iteration logic
Here certain module is executé repeatedly until condition satisfies.
At first, the body of loop i.e. module will be executed with K=R and then with K = R + T, then with K = R + 2T and so on until K = S. The loop ends when K > S.
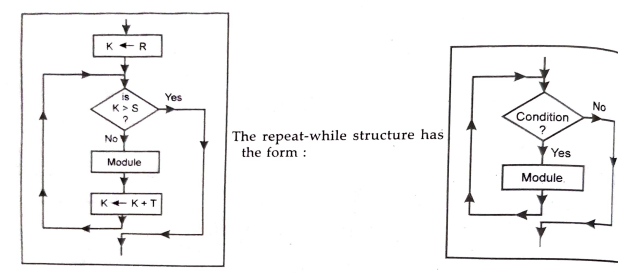
Here module is executed until the condition is satisfied.
Q. 10 Write an algorithm to find solutions of quadratic equation Ax² + Bx + C = 0 where A ≠ C
Ans : The algorithm inputs the coefficients A, B, C of a quadratic equation and outputs the result: solution, if any.

ARRAY
Q.11 What are linear arrays ?
Ans : A data structure is said to be linear if its elements form a sequence.
A linear array is the data structure which consists of finite, ordered set of homogeneous data elements such that :
1. The elements of the array are referenced respectively by an index set (subscript) consisting of ‘n’ consecutive numbers.
2. The elements of the array are stored respectively in successive memory locations.
3. The number ‘n’ of the elements is called length or size of array.
In general, the size or length of the array can be obtained from the index set by the formul:-
Length = UB - LB +1
where UB - the largest index called Upper Bound.
LB - the smallest index called Lower Bound.
e.g. Let DATA be 5 element linear array as follows :

The element of an array may be denoted by the subscript notation such that :
DATA [3] = 600
In C++, array is declared as -
int data [100]; which specify an array data of 100 integers.
Q. 12 How arrays are represented in memory ?
Ans :
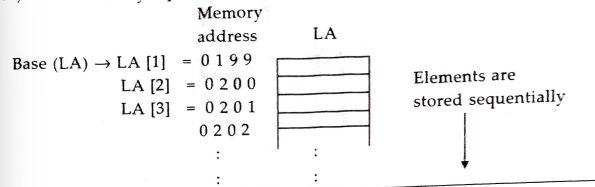
i) The elements of linear array are stored in consecutive memory locations.
ii) Computer does not need to keep track of the address of every element of array. It just requires the address of first element of array, LA, denoted by Base (LA) and called the base address of linear array LA.
iii) Using this base address, the computer calculates address of any element of array by using the formula.
LOC (LA[K]) = Base (LA) + W (K - LB)
where,
LOC (LA[K]) is address of Kth element of LA
W is number of words per memory location for LA
and LB is lower bound i.e, smallest index of LA.
iv) The memory representation of an array is shown in figure below :
Q. 13 Consider the array AUTO, which records number of automobiles from 1932 through,1984. Suppose Base (AUTO) = 200 and W = 4 words.
Then,
LOC (AUTO [1932]) = 200, LOC (AUTO [1933]) = 204
LOC (AUTO [1934]) = 208
Calculate address at which 1965's record is stored.
Ans :
Given:- K = 1965
Base address = 200
W = 4
LB = 1932
The address of the array element for the year 1965 can be obtained -
LOC (AUTO [1965]) Base (AUTO) + W (1965 - LB)
200 + 4 (1965 - 1932) = 332
Q.14 What is traversing an array ? Give the algorithm for traversing a linear array?
Ans : Traversing an array means accessing with each element of array only at once, so that can be processed.
Algorithm : Traversing a linear array.
Here LA is a linear array with lower bound LB and upper bound UB. Following algorithm apply operation PROCESS to each element of LA.
Step 1: [Initialize counter]
set K: = LB
Step 2: Repeat steps 3 and 4 while K <= UB :
Step 3: [Visit element]
Apply PROCESS to LA[K]
Step 4: [Increment counter]
set K := K + 1
[End of step 2 loop]
Step 5: Exit
OR
This algorithm traverses a linear array LA with lower bound LB and upper bound UB.
Step 1: Repeat FOR K= LB To UB:
Apply PROCESS to LA[K]
[End of loop]
Step 2: Exit
Q. 15 What is inserting ? Write an algorithm for inserting an element to a linear array.
Ans :
i) Inserting refers to the operation of adding an element to the existing elements of array.
ii) The element can be easily inserted at the end of array. But for insertion in the middle of array, it is required to move the elements of array one byte forward.
iii) The following algorithm inserts a data element ITEM into the kth position in an array LA with N elements.
Algorithm :
INSERT (LA, N, K, ITEM)
Here LA is a linear array with N elements and K is a positive integer, such that K <= N. This algorithm inserts an element ITEM at Kthposition in LA.
Step 1: [Initialize counter]
Set J: = N
Step 2: Repeat steps 3 and 4 while J >= K:
Step 3: [Move Jth element forward ]
Set LA[J + 1]: = LA[J]
Step 4: [Decrement counter]
Set J := J - 1
[End of step 2 loop]
Step 5: [Insert the element]
Set LA[K] := ITEM
Step 6: [Reset N]
Set N := N + 1
Step 7: Exit
Click on DOWNLOAD and Data Structures Part - 2 pdf will start downloading.
-
Can I download Data Structures Part - 2 PDF Free ?
Yes, you can download all TPS Computer Science 12th Pdf for free. Only you need to click on download button and wait for 30 seconds. Your download will start automatically.
-
Unable to download the pdf ?
Please click on the download button and wait for 30 seconds for the downloading link to be generated. After that check your downloads you will get your pdf.
-
Why I am seeing count down timer after clicking on download button ?
Please wait for it to complete and then you will able to download it. You are seeing count down timer for downloading link to be generated.

